Sai phạm trong sử dụng mật mã khóa công khai
Có một giả thiết quan trọng được mặc định để bảo đảm độ an toàn của hạ tầng khóa công khai, đó là khi thiết lập khóa, không được lặp lại các lựa chọn ngẫu nhiên trước đó, ví dụ, với hệ mật RSA thì modulus của hai người phải khác nhau, không một tham số nào trong hai tham số p, q được dùng chung. Trước đây đã xảy ra một lỗi nghiêm trọng trong lệnh sinh số ngẫu nhiên của Debian OpenSSL, khiến cho những khóa RSA được sinh ra từ đó mắc phải điểm yếu được nói tới ở trên. Người ta đã phải lập một “danh sách đen” các modulus như vậy và cộng đồng những người làm mật mã đã tốn khá nhiều công sức để khắc phục sự cố này (xem [3, 4, 5]).
Được tài trợ bởi Quỹ Khoa học Quốc gia Thụy Sỹ, các tác giả của công trình nghiên cứu (Lenstra và các cộng sự) [1] đã thu thập dữ liệu và thực hiện phân tích, thống kê các khóa công khai. Mục tiêu chính của họ là kiểm chứng tính hiệu lực của giả thiết mà các lựa chọn ngẫu nhiên khác nhau đã thực hiện mỗi khi các khóa được sinh ra và họ đã rút ra được rất nhiều nhận xét hữu ích.
Thu thập dữ liệu và kết quả xử lý
Được sự giúp đỡ của trạm quan sát SSL thuộc Quỹ tổ chức điện tử (một dự án khảo sát các chứng thư điện tử dùng để bảo mật các website), đến tháng 11/2011, Lenstra và các cộng sự đã thu thập được số liệu như sau:
- Trong 6.185.372 chứng thư số X.509 có 6.185.230 chứng thư số chứa một cặp RSA (modulus và lũy thừa), cùng với 141 khóa công khai DSA và duy nhất một điểm ECDSA trên đường cong đã được NIST chuẩn hóa secp384r1; 47,6% số các chứng thư số có ngày hết hạn sau năm 2011; Khoảng 77,7% các chữ ký chứng thực sử dụng SHA- 1 hoặc tốt hơn (5.287 dùng SHA- 256, 24 dùng SHA- 384, 525 dùng SHA- 512), 22,3% dùng MD5 và các hàm băm khác (122 dùng MD2, 30 dùng GOSTHASH, 14 dùng MD4 và 9 dùng RIPEM160); 33,4% số các chứng thư thỏa mãn cả hai yêu cầu là có thời gian hết hạn sau năm 2011 và sử dụng hoặc SHA- 1/SHA- 2.
- 5.481.332 khóa PGP (không dùng kèm hàm băm và không bị hết hạn), trong đó: 1.546.752 (46,5%) là các khóa công khai ElGamal; 2.536.959 (46,3%) là các khóa công khai DSA; còn lại 397.621 (7,3%) là các khóa công khai RSA.
Lenstra và các cộng sự đã phân tích các khóa cho ElGamal, DSA và ECDSA. Nhưng ở đây, chúng ta chỉ nghiên cứu chi tiết vào gần 6,6 triệu khóa RSA (6.185.230 + 397.621 = 6.582.851).
Các số mũ công khai: Bảng 1 liệt kê 10 số mũ công khai thường xuyên xuất hiện nhất của chúng trong các khóa RSA trong các chứng thư số X.509, các khóa PGP và khi cả hai được kết hợp. Đã phát hiện ra một số dị thường đối với các khóa PGP RSA đó là có 8 lần e = 1 và hai giá trị e chẵn.
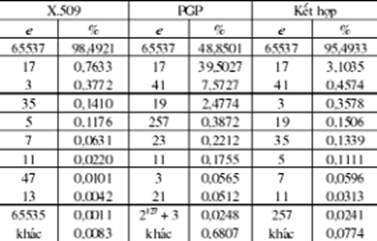
Debian moduli: Hai trong số các giá trị n, một số 1024 bit và một số 2048 bit, mỗi số gặp 1 lần, đã bị loại bỏ, bởi vì nó có thể bị phân tích hoàn toàn nhờ dữ liệu từ một báo cáo [3]. 30.097 giá trị n khác (chiếm 0,48% cùng với 21.459 giá trị khác nhau) đã được liệt vào danh sách đen [4], nhưng do các thừa số của chúng là không dễ có được nên chúng được giữ lại.
Các modulus chung: Đã phân loại một tập gồm 6.185.228 chứng thư số X.509 thành các cụm (cluster), trong đó các chứng thư số chưa cùng modulus RSA được xếp vào cùng một cluster. Thống kê cho thấy, một số đáng kể các cụm chứa hai hoặc nhiều hơn các chứng thư số, chẳng hạn: Có một cụm với 16.489 chứng thư số, có tổng cộng 14 cụm với nhiều hơn 1 nghìn chứng thư số (với các kích thước 8366, 6351, 5055, 3586, 3538, 2645, ....); Có 5.055 cụm dùng chung các modulus được liệt vào danh sách đen. Số các trường hợp tốt gồm 5.918.499 modulus (các cụm chỉ có 1 chứng thư).
Các modulus khác nhau: Như đã thấy ở trên, 5.989.523 giá trị n khác nhau được trích ra từ các chứng thư số X.509. Tương tự 397.590 (397.621 – 59 + 28) giá trị n của PGP là duy nhất. Do có 129 giá trị n được chứa trong cả 2 tập, nên tổng cộng có 6.386.984 (gần 6,4 triệu) giá trị n khác nhau. 129 giá trị n được chứa trong cả hai tập xảy ra trong 204 chứng thư số X.509 và trong 137 khóa PGP.
Kích thước modulus: Kích thước của 6.386.984 giá trị n thu thập được như sau: kích thước nhỏ nhất 374 bit xảy ra 1 lần; 0,01% có kích thước 384 bit; 1,6% số các giá trị n có kích thước 512 bit. Một số lớn các modulus 512 bit đã được chứng thực sau năm 2000 và thậm chí gần đây; 0,8% có kích thước 768 bit. Kích thước chung nhất là 1024 bit có 73,9%; còn 2048 bit chiếm 21,7%.
Kiểm tra tính nguyên tố, các thừa số nhỏ và các phép kiểm tra khác: Đã phát hiện một số dị thường: Hai trong số các giá trị n mà xuất hiện 1 lần là nguyên tố, 171 giá trị n có một thừa số < 224 (với 68 giá trị n chẵn). Cả 173 giá trị n trên không tuân theo các chuẩn để sinh các modulus RSA [2] và chúng bị bỏ đi. Phương pháp phân tích số của Fermat (hoạt động nếu hai thừa số là gần nhau) không tạo ra thừa số nào. Không tìm thấy modulus nào như đã được thông báo bởi Mike Wiener (n = pq, với p nguyên tố và q là số nguyên tố nhỏ nhất mà lớn hơn so với p.
Các modulus với các thừa số chung: Nếu các modulus có chung một thừa số nguyên tố thì sẽ làm giảm hoàn toàn độ an toàn đối với tất cả các modulus cùng tham gia vào. Nhóm tác giả đã sử dụng công cụ của lý thuyết đồ thị (trong đó các thừa số p,q được đồng nhất với các đỉnh đồ thị, còn modulus đồng nhất với các cạnh của đồ thị) để phân tích các kết quả và đã tìm ra:
- 1.995 thành phần liên thông (mà mỗi thành phần bao gồm ít nhất 2 cạnh), có 3 hoặc nhiều hơn các đỉnh. Trong đồ thị có một số đáng kể các cạnh có tính bội cao hơn 1. Trong số 1.995 thành phần liên thông, 1.988 là các “cây” có độ sâu bằng 1. Một cây có độ sâu bằng 1 chứa một đỉnh gốc và các cạnh dẫn tới các đỉnh khác. Trong số các cây có độ sâu 1 thì phần lớn có 2 hoặc 3 “lá”: 1.200 cây có 2 lá (tức là, 1.200 cặp của các giá trị n, mỗi cặp có chung một số thừa số nguyên tố khác nhau), 345 cây có 3 lá.
- 497 trong số 1988 cây có độ sâu bằng 1 có ít nhất một cạnh tương ứng với một modulus RSA xảy ra tại ít nhất 2 chứng thư số X.509 hoặc khóa PGP. Trong 1.491 cây có độ sâu bằng 1 khác, tất cả các tính bội của cạnh đều là 1. Một cây duy nhất có độ sâu 1 mà có tới 4.627 lá (tức là, 4.627 giá trị n cùng có chung một thừa số nguyên tố).
Hai giá trị n bất kỳ liên kết với các cạnh trong cùng một cây độ sâu 1 thì có thể sẽ bị phân tích. Hai giá trị n mà được liên kết với các cạnh khác có thể được phân tích nếu các cạnh là kề nhau (tức là có chung đỉnh), hoặc người ta tìm thấy một đường dẫn nối chúng lại. Kết quả phân tích cho thấy có 12.934 modulus RSA khác nhau không đảm bảo độ an toàn. Các khóa bí mật của chúng là có thể truy cập được với cách thức Lenstra đã làm. Nó ảnh hưởng tới 21.419 chứng thư số X.509 và khóa PGP. Phần lớn các chứng thư này đã hết hạn hoặc sử dụng MD5 như hàm băm. Nhưng 5.250 chứng thư số bao gồm 3.201 modulus RSA 1024 bit khác nhau vẫn còn hợp lệ, chúng sử dụng SHA - 1, và vẫn có thể đang trong quá trình lưu hành. Trong số đó, 727 là các chứng thư số tự ký và đã được sử dụng để ký các modulus RSA khác. Tóm lại, trong dữ liệu RSA 1024 bit đã thu thập được thì 99,8% đảm bảo an toàn ở mức tốt nhất (0,2%).
Các modulus RSA và các chứng thư số bị ảnh hưởng: 1.995 thành phần liên thông đã nói tới ở trên chứa tổng cộng 14.901 đỉnh và 12.934 cạnh: khi phân tích hoàn toàn 12.934 (0,2%) giá trị n khác nhau sẽ cho ra 14.901 số nguyên tố khác nhau.
- Có 11.699 giá trị n được sử dụng làm modulus RSA trong chứng thư số X.509 hoặc khóa PGP duy nhất và 1.235 giá trị gặp nhiều hơn 1 lần trong tổng cộng 9.720 chứng thư số và khóa. Do vậy, 21.419 (11.699 + 9720) chứng thư số X.509 và khóa PGP bị ảnh hưởng. Các modulus bị ảnh hưởng là những modulus được dùng chung nhiều hơn nhiều so với các modulus khác và không có modulus bị ảnh hưởng nào đã bị ghi vào danh sách đen.
- Trong 14.901 số nguyên tố có 14.592 số dài 512 bit, 307 số dài 256 bit và 2 số còn lại dài 257 bit.
- Trong số 12.934 giá trị n có 214 giá trị dài 512 bit, 12.720 giá trị dài 1.024 bit.
- Trong số 214 giá trị n dài 512 bit có 47 giá trị xảy ra như các modulus RSA trong 188 chứng thư số X.509 mà chưa hết hạn và sử dụng SHA-1 như hàm băm.
- Trong số 12.720 giá trị n dài 1.024 bit, có 3.201 giá trị là các modulus RSA trong 5.250 chứng thư số chưa hết hạn và sử dụng SHA - 1 làm hàm băm. Trong số chứng thư này có:
+ 617 là các chứng thư số bình thường không được tự ký (non self- signed) của người sử dụng đầu cuối với “CA = false” (cùng với 390 modulus RSA khác nhau).
+ 4.633 chứng thư còn lại chứa 2.811 modulus RSA khác nhau có “CA = true” và được tự ký, trong số chúng có 727 chứng thư (với 304 modulus RSA khác nhau) đã được sử dụng để chứng thực các modulus RSA khác (nhưng không có trong bộ sưu tập các modulus bị ảnh hưởng). 727 chứng thư này có chung trường “issuer” (“người phát hành”) và cả 304 modulus RSA xảy ra trong các cây độ sâu 1 không chứa modulus được những người khác sở hữu. Cho nên, vấn đề mất an toàn này được kiềm chế một cách hợp lý.
Một số đánh giá
Trên cơ sở các số liệu thu thập và kết quả xử lý của các tác giả [1], có thể rút ra một số kết luận như sau:
- Đã tìm thấy khoảng 0,2% các khóa công khai cần phải lưu ý xem xét lại. Đáng ngạc nhiên về mức độ mà các khóa công khai được dùng chung bởi những người sử dụng không có liên quan đến nhau. Đặc biệt là hàng nghìn modulus RSA 1024 bit, trong đó có hàng nghìn số ở trong các chứng thư X.509 vẫn còn thời hạn sử dụng nhưng không đảm bảo an toàn.
- Việc sinh khóa trong thế giới thực cho các hệ mật “dùng nhiều số bí mật” như RSA là nguy hiểm hơn đáng kể so với cho các hệ mật “dùng số bí mật duy nhất” như ElGamal hoặc (EC)DSA dựa trên Diffie- Hellman.
- Do tính chất toán học đặc thù của RSA nên cần phải cẩn thận hơn trong quá trình sử dụng, bởi các nguyên nhân sau:
+ Thứ nhất, RSA cần đến 2 số nguyên tố ngẫu nhiên để tạo ra khóa bí mật, trong khi những hệ dựa trên độ khó của bài toán logarit rời rạc chỉ cần 1 yếu tố ngẫu nhiên.
+ Thứ hai, thuật toán Euclid có độ phức tạp thấp nên đôi khi cho phép phá được RSA.
+ Thứ ba, đối với hệ mật như ELGamal, DSA hay ECDSA thì còn có những tham số mang tính “hệ thống” như nhóm hữu hạn được xét đến, phần tử sinh cho nó, tham số cho đường cong ellip,... còn hệ mật RSA thì không có.
+ Sinh modulus RSA đúng chuẩn mực bao gồm việc tìm 2 số nguyên tố ngẫu nhiên. Nó cần phải được làm theo một cách thức, sao cho những số nguyên tố này chưa được chọn trước đây. Xác suất để không sinh lại một số nguyên tố sẽ tương ứng với mức an toàn, nếu khuyến cáo của NIST được tuân thủ thì cần sử dụng một mầm ngẫu nhiên có độ dài bit gấp 2 lần mức an toàn dự kiến. Điều này cho thấy, trên thực tế khuyến cáo này không phải luôn được tuân thủ. Không phụ thuộc vào cách mà các số nguyên tố được lựa chọn, việc nạp mầm khởi đầu không tốt, có thể dẫn tới các rủi ro và hệ quả là các khóa sẽ bị lặp lại nếu không có entropy cục bộ “tươi” được sử dụng. Thậm chí có thể với hai mầm khác nhau nhưng lại cho cùng một kết quả đầu ra.
Các tác giả của công trình nghiên cứu đã nêu [1] cũng cho thấy rằng, còn nhiều điểm chưa giải thích được: tần xuất tương đối và sự xuất hiện của những trùng lặp; tại sao một số thành phần liên thông có thể xuất hiện được; không có tương quan giữa thời gian chứng thực và tính bị tổn thương của các khóa được phát hiện ra.
Như vậy, mật mã khóa công khai có nhiều tiện lợi, nhưng dùng thế nào cho đúng là vấn đề còn rất phức tạp